벨만-포드 알고리즘이란?
벨만-포드 알고리즘은 그래프에서 특정 시작 노드로부터 다른 모든 노드까지의 최단 경로를 구할 때 사용하는 알고리즘입니다.
특히, 가중치가 있는 그래프에서 최단 경로를 구하기 위해 사용할 수 있습니다.
특징
벨만-포드 알고리즘의 특징은 다음과 같습니다.
- 가중치가 음수인 그래프를 처리할 수 있다.
- 음수 사이클이 있는 경우를 식별할 수 있다.
- 시간 복잡도는 O(NM)이다. (N은 노드의 수, M은 간선의 수).
벨만-포드 알고리즘 동작
벨만–포드 알고리즘은 노드의 수가 N개일 때, 모든 간선을 최대 N−1번 반복하며 최단 경로의 길이를 갱신합니다.
노드가 N개인 그래프에서 사이클을 포함하지 않는 최단 경로는 최대 N−1개의 간선으로 구성될 수 있기 때문에,
N-1번의 라운드를 거치며 모든 간선을 확인하면 최단 경로의 길이가 결정됨을 보장할 수 있습니다.
예를 들어, 다음과 같이 N=3인 경우 노드 사이의 최대 거리는 2입니다.

본격적으로, 벨만-포드 알고리즘의 동작을 알아보겠습니다.
1번부터 5번까지 총 5개의 노드가 존재하고, 각 간선은 가중치를 갖고 있습니다.
이때, 총 4번(N-1번)의 라운드를 반복하며 모든 간선을 확인합니다.
이때 현재 노드를 거쳐 가는 것이 기존 경로보다 더 작다면 최단 거리를 갱신합니다.
1. 초깃값 설정

시작 노드인 1번 노드의 거리는 0으로, 나머지 노드들은 아직 경로를 알 수 없으므로 INF(무한대)로 설정합니다.
2. 모든 간선 탐색 및 거리 갱신

모든 간선을 하나씩 확인하며 거리를 갱신합니다.
이때, 이미 경로가 알려진 노드(거릿값이 INF가 아닌 노드)에서 출발하는 간선들만 갱신을 수행할 수 있습니다.
거릿값이 INF인 노드는 아직 도달할 수 없는 상태이므로, 해당 노드에서 출발하는 간선은 최단 거리 갱신에 영향을 주지 않습니다.
위에서, 시작 노드(1번)의 거리가 INF가 아닌 0이므로, 1번과 연결된 2,3,4번 노드의 최단 거리가 갱신됩니다.

다음으로, 기존에 1번 노드에서 4번으로 직접 가는 거리는 7이었습니다.
하지만 3번 노드를 거쳐 가는 경로(1 -> 3 -> 4)를 확인해 보면, 가중치의 합이 4로 기존값인 7보다 작아 새롭게 최단 경로가 갱신됩니다.
또한, 5번 노드의 최단 경로도 갱신되었습니다.

마지막으로 4번->5번 노드로 이어지는 간선을 통해 5번 노드로의 최단 경로가 6으로 갱신되었습니다.
N-1번의 라운드가 종료되면, 시작 노드로부터 그래프 내의 모든 노드에 도달하는 최단 경로의 길이가 결정됩니다.
음수 사이클 판별
추가로, 벨만-포드 알고리즘을 사용하면 그래프 경로의 길이가 음수인 사이클이 있는지를 확인할 수 있습니다.
음수 사이클을 포함하는 경우 경로의 길이는 무한히 짧아질 수 있으므로, 최단 경로를 구할 수 없습니다.
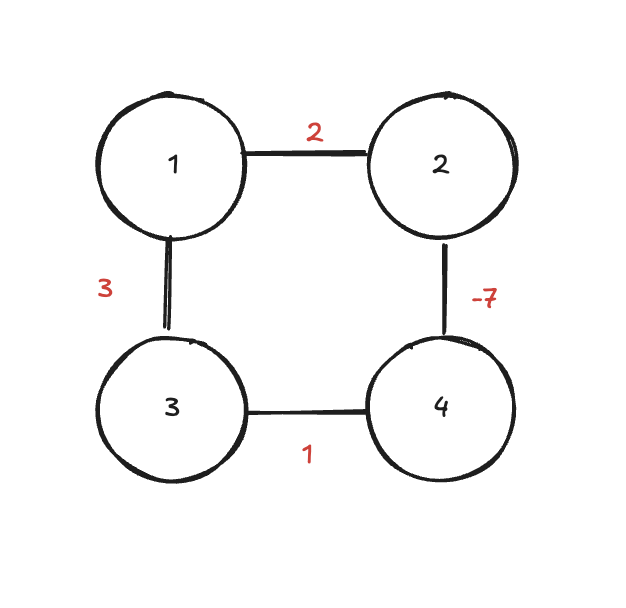
예를 들어, 위와 같은 그래프에서 (2 -> 4 -> 3 -> 1 -> 2)인 경로의 길이는 -1입니다.
해당 사이클을 한 바퀴 돌 때마다 최단 경로의 길이는 -1씩 감소하게 됩니다.
이러한 음수 사이클을 식별하기 위해서는 N번째 라운드를 추가로 실행해야 합니다.
앞서 살펴보았듯이, 노드가 N개인 그래프에서 사이클이 없는 최단 경로는 최대 N-1개의 간선으로 구성되어, N-1번의 라운드를 거치면 모든 노드까지의 최단 거리는 확정되고, 그 이후 N번째 라운드부터는 아무리 반복하더라도 거릿값이 갱신되지 않습니다.
하지만 음수 사이클이 존재한다면, 사이클을 돌 때마다 최단 거리는 계속해서 작아지게 되어 최단 경로를 구할 수 없습니다.
정리해 보면, N번째 라운드를 실행해서 노드의 최단 경로가 줄어드는 경우가 있다면, 그래프에 음수 사이클이 있다고 판단할 수 있습니다.
코드
class Edge {
int from;
int to;
int weight;
public Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
}
출발 노드, 도착 노드, 간선의 가중치를 저장하기 위한 Edge 클래스를 작성합니다.
static final Integer INF = Integer.MAX_VALUE;
static int N,M;
static ArrayList<Node> graph;
static int[] distance;
public static void main(String[] args) throws IOException {
N = 5;
M = 7;
graph = new ArrayList<>();
distance = new int[N + 1];
//최단 경로의 초깃값을 INF로 설정한다.
Arrays.fill(distance, INF);
graph.add(new Node(1, 3, 3));
graph.add(new Node(1, 4, 7));
graph.add(new Node(1, 2, 2));
graph.add(new Node(3, 4, 1));
graph.add(new Node(2, 4, 3));
graph.add(new Node(2, 5, 5));
graph.add(new Node(4, 5, 2));
bellmanFord(1);
}
- INF 상수 : 도달할 수 없는 경로를 표시하기 위한 수로, 알고리즘 조건에 맞는 충분히 큰 값을 설정합니다.
- graph : 간선의 정보를 저장하는 리스트이다.
- distance : 해당 노드까지의 최단 경로를 저장하기 위한 배열입니다.
static void bellmanFord(int start) {
distance[start] = 0;
for (int i = 1; i < N; i++) {
for (Node node : graph) {
if (distance[node.from] != INF) {
distance[node.to] = Math.min(distance[node.to], distance[node.from] + node.weight);
}
}
}
}
벨만-포드 알고리즘입니다.
시작 위치의 최단 거리는 0으로 설정하며, 총 N-1번의 라운드를 진행하며 모든 간선(M개)을 확인합니다.
현재 노드(to)까지 알고 있던 기존의 최단 거리보다, 특정 노드(from)를 거쳐서 오는 경로가 더 짧을 경우 그 값을 최솟값으로 갱신합니다.
'알고리즘' 카테고리의 다른 글
| [소프티어] 금고털이 - JAVA (0) | 2025.01.20 |
|---|
